←旧ロゴ、今は文字ロゴに変わった。お次はダイソー。
ここもロゴが変わって久しい。
これも面積の計算をしていきたいと思う。
←旧ロゴ、今は文字ロゴに変わった。
今回は以下の図形とする（相当簡略化した）。
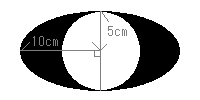
楕円Aと正円Bがあり、楕円Aの中に正円Bが入っている。両円の中心は同じで、正円Bの半径は5cm、楕円Aの長いほうの半径が10ｃｍ、短いほうが正円Bと同じ5cmであるとする。そして、今回は楕円Aから正円Bを引いた面積を求めてみよう。
今回、楕円が絡んでくる。正式な証明方法とかは高校数学の範囲（正弦定理とか余弦定理とかなんかそういうのがいっぱい出てくる）だが、公式は
である。平たく言えば。
とりあえず、これで進める。
正円（楕円に対して、縦半径と横半径が同じ円のことを、正円もしくは真円という）Bの面積は、前回でもいったように、半径×半径×円周率だから、
5×5×3.14＝25×3.14
＝100÷4×3.14
＝314÷4
＝78.5
である。
それに対して、楕円Aは、
10×5×3.14＝50×3.14
＝100÷2×3.14
＝314÷2
＝157
である。
よって、それを引いた黒い部分の面積は、
157-78.5＝78.5
である。