←かつてのダイエーのロゴ昔懐かしいダイエーのロゴ。
いや、現在もありますよ、ダイエーの店舗自体は。
ただ、全盛期の勢いはもうありませんけど、
イオン（ジャスコ）の傘下になっちゃいましたけど。
←かつてのダイエーのロゴ
現在のダイエーのロゴ→
そんな懐かしい（？）ダイエーのロゴの面積を語ろう。
まず、忘れてる方も多いかと思うが円の面積の公式は、
だ。
もしここを読んでいる読者が小学生なのであれば、πではなく3.14で覚えておいたほうが身のためだ。
中学生以上であれば、「半径の2乗×π」で分かってもらえると思う。
なお、円周の長さは「直径×3.14（π）」だ。
そして、扇形の面積の公式は、
である。
そして、今回は以下の様な図形だとしよう。
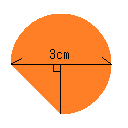
直径3cm（半径1.5cm）の円、うち90度の直角三角形で削り取られる形とする。
まず、直径3cm（半径1.5cm）の円の面積は、
1.5×1.5×3.14（π）＝2.25×3.14
＝4.5×1.57
＝9×1.57÷２
＝（10-1）×1.57÷２
＝（15.70-1.57）÷2
＝14.13÷2
＝7.065（2.25π）(cm)
となる。おとなしく電卓を使っても良かったが、ここは中学受験を希望する方々のためにも（？）、工夫して解いてみた（どうでもいい余談だが、良い子のみんなはちゃんと途中式を書こう。書かないとあってても当てずっぽうで答えたと思われ減点にされる可能性もあるし、間違っていても部分点がもらえる可能性が出てくる）。
さて本題。
この上の「ダイエー」、よく見ると形が90度の直角三角形と、270度の扇に分かれているのがわかるだろうか。
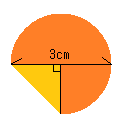
そうなれば話は簡単だ。それを別々に分けて計算すればいいのだから。
まずは、扇の方から解いてみよう。扇の中心角は270度だから、先ほどの円の面積に4分の3をすればよい。
また、直角三角形の部分は角の一辺が1.5cmなので、おなじみ「底辺×高さ÷２」をすればよい。
したがって、
（7.065×3/4）+（1.5×1.5÷２）＝（14.13+7.065）÷4+（2.25÷２）
＝21.195÷4+1.125
＝5.29875+1.125
＝6.42375（cm）
となる。
とりあえず、ダイエーの面積の公式は、
となる。
いまや（2019年現在）ロゴが変わって数年経つ世代が受験するという現代、よもやダイエーを問題に出すことはないと思われる。
しかし、この考えは頭の片隅にでも入れておいてもらいたい。
終わり